Rosabelen Blog: G4G

Mostrando entradas con la etiqueta G4G. Mostrar todas las entradas

Variaciones sobre una cáscara de banana

(Éste es el resumen de mi charla en el 5to. Encuentro para Celebrar el Ingenio de Martin Gardner y Jaime Poniachik.)

..............

Adenda del 8/11/14: Conjeturo que la suma máxima en el cuadrado de $n\times n$ es aproximadamente igual a $\frac{n^3}{2}$. Predigo en consecuencia que para 8x8 la suma máxima es aproximadamente igual a 256.

Comentario del 4/2/15: Marcos ha encontrado una suma máxima para 8x8 de 258, tal vez mi conjetura no sea tan acertada.

Adenda del 30/1/15: Al final de la entrada he agregado otra solución que me ha hecho llegar Marcos.

..............

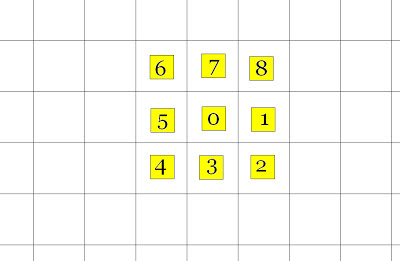
En el movimiento cáscara de banana (1) una pieza resbala (hacia arriba, hacia abajo, hacia la derecha o hacia la izquierda) tanto como le sea posible, es decir, hasta que llega al borde del tablero o hasta que choca contra una casilla anulada. En el primer desafío elegimos una casilla inicial cualquiera, colocamos una pieza y marcamos allí un 0 (las casillas donde anotamos números se convierten en anuladas). A continuación, comenzamos a mover la pieza anotando, cada vez, en la casilla de llegada cuál ha sido la distancia recorrida. Por ejemplo:

Así seguimos hasta que la ficha ya no se puede mover. Para tableros de 3x3, 4x4, 5x5,… hay que lograr:

1) Que al trabarse el movimiento, la suma de los números sea la MENOR posible.

2) Que se complete el tablero y que a la vez la suma sea la MENOR posible.

3) Que se complete el tablero y que a la vez la suma sea la MAYOR posible.

Como segundo desafío transformamos este mecanismo en un juego para dos jugadores, digamos Alicia y Bruno. Alicia juega primero y elige una casilla inicial cualquiera (que queda anulada), luego Bruno desplaza la ficha y la casilla final queda igualmente anulada; así siguen hasta que el juego se traba. Quien haya hecho la última jugada, gana. Para tableros de 3x3, 4x4, 5x5,… la pregunta es: ¿Cuál de los dos jugadores tiene una estrategia ganadora? También podemos preguntarnos qué sucede en la versión de “el último que juega pierde”.

Nota:

(1) No sé si el mecanismo, pero sí su nombre, hasta donde conozco, se debe a Jaime Poniachik. [Según comentó Pablo Milrud en el propio encuentro, el mecanismo "cáscara de banana" -y tal vez también el nombre- serían en realidad creaciones de Iván Skvarca.]

Resumen de las soluciones recibidas hasta ahora (véanse más abajo los detalles):

Para la pregunta 1) la respuesta es 5 independientemente del tamaño del tablero, siempre que sea mayor que 2 (respuesta enviada por Rodolfo Kurchan).

Para las preguntas 2) y 3):

3x3: Mín = 12, Máx = 12. (Rodolfo Kurchan)

4x4: Mín = 23, Máx = 30. (Rodolfo Kurchan)

5x5: Mín = 41, Máx = 61. (Marcos Donnantuoni)

6x6: Mín = 68, Máx = 107. (Marcos Donnantuoni)

7x7: Mín = 99, Máx = 174. (Marcos Donnantuoni)

8x8: Mín = 142. Máx = 258. (Marcos Donnantuoni)

Para el juego de dos, Rodolfo demostró que en tableros de 3x3 y 5x5 gana el primero.

Detalles:

(26/10/14) Pocas horas después del evento, Rodolfo Kurchan envió estas soluciones:

Para la pregunta 1 me parece que para cualquier tablero de lado nxn (salvo 2x2 que es muy chico) se traba con suma 5:

.0.

11.

12.

Ésta es la "punta" de cualquier tablero, va de 0 a 2, al 1 de arriba, al 1 de la izquierda y al 1 de abajo.

Para las preguntas 2 y 3:

3x3 mínimo 12, máximo 12

4x4 mínimo 23, máximo 30

1131 0313

2011 2113

1113 3221

3211 3113

Para el juego:

Tablero de 3x3 y 5X5 gana el primero

...

.12

453

76...

OX...

891..

453..

..2..

X es la jugada 10 y O es la jugada 11 (si el segundo jugador luego de A5 va para abajo pierde en 7 movidas en lugar de en 11.

(29/10/14) Marcos Donnantuoni envía estas soluciones (aclara que sin garantía de que sean óptimas):

5x5 min

41

← ↑ ↓ → ↑ ← ↓ → ↑ ← ↓ → ← ↑ → ↓ ← ↓ → ↑ → ← ↑ ↓

2 3 1 1 1

1 1 2 2 4

1 0 1 2 1

4 1 1 2 1

1 1 4 1 2

5x5 max

61

↑ ← ↓ → ← → ↑ ↓ ← ↑ → ↓ ← → ↑ ← ↑ → ↓ ↑ ↓ ↑ ← ↓

4 1 1 4 3

2 2 3 1 4

4 1 1 3 1

3 1 2 3 0

4 3 4 2 4

6x6 min

68

→ ↑ ↓ ↑ ← ↑ → ↓ ↑ ← ↑ → ← ↓ → ↑ ← ↓ → ↑ ← ↓ → ← ↓ → ↓ ← ↑ ← ↑ → ↓ ← ↓

1 1 1 2 4 3

5 3 3 1 1 1

1 3 1 1 2 2

1 2 1 3 0 1

5 1 1 1 3 1

1 1 5 1 1 3

6x6 max

107

↓ ← → ↑ ← ↓ → ↑ ← → ↓ ↑ → ↓ ← → ← ↑ → ↓ ↑ ↓ ← ↓ → ↑ ↓ ↑ ↓ → ↑ ← → ← ↑

4 3 5 2 5 0

5 1 3 4 4 3

3 1 2 1 2 1

5 3 2 1 4 1

4 2 4 3 3 5

5 1 1 5 4 5

7x7 min

102

↓ → ← ↑ → ↓ ← ↑ → ↓ ↑ ↓ ← ↓ ↑ ↓ → ↓ ← → ↑ ← ↓ ↑ → ↑ ← ↓ → ← ↑ → ↓ ← ↑ ↓ ↑ → ← ↓ ← ↑ → ↑ ↓ → ← ↑

2 3 6 1 1 6 1

1 1 1 2 4 4 1

2 2 2 1 2 1 2

6 4 1 1 2 1 1

2 1 1 4 1 2 3

1 1 4 3 0 1 5

3 2 1 1 1 1 2

7x7 max

172

← ↓ ↑ → ↓ ← ↑ → ↓ ↑ ↓ ← ↑ → ↓ ↑ ← ↓ → ← ↑ → ↓ ← ↑ → ← ↓ ↑ ↓ ← → ↑ ↓ → ↑ ← ↓ → ← ↑ → ↓ ↑ ↓ ← ↑ ↓

6 6 6 1 2 4 0

5 3 4 5 3 5 6

3 4 1 2 2 2 6

6 1 3 1 2 4 2

1 5 3 1 1 3 6

5 2 1 4 3 4 3

6 5 2 6 5 6 5

(30/1/ 15) 8x8 max

250

→ ↑ ↓ ↑ ↓ ← ↑ → ↓ ↑ ↓ ← → ↑ ← ↓ → ← → ↑ ↓ ↑ ← ↓ → ↑ ← ↓ → ← ↓ ↑ → ↓ ← → ↑ ↓ ← ↑ → ↓ ↑ ← → ↓ → ↑ ← → ← → ↓ ← ↓ → ↑ ↓ ↑ → ← ↓ ←

5 4 4 1 7 6 6 7

4 2 1 6 5 4 6 5

7 5 3 4 2 4 1 2

1 6 2 2 1 2 4 7

3 2 3 1 1 3 5 7

7 5 2 3 3 4 1 4

6 3 1 1 6 5 5 6

0 7 3 7 2 4 7 7

7x7 min

99

1 6 1 1 2 6 1

1 4 4 1 2 4 1

1 3 1 1 1 2 6

2 1 1 3 1 1 3

4 2 2 0 2 3 1

3 1 1 1 1 1 2

1 1 2 2 2 1 4

↓↑←↓→←↑←↓→↓←↑←↓↑→↓←→↑→↓←↑→←↓→↓↑←↓→↑↓↑↓←↑↓←↓↑→↑→↑

7x7 max

174

0 4 2 6 4 6 6

4 5 5 4 2 4 5

6 4 2 2 3 1 2

1 5 1 1 2 1 6

3 4 1 3 3 3 6

6 2 3 5 2 4 4

6 6 6 1 1 5 6

→↓←→↑←↓↑→↓←↑↓→↑←↓→←↓→↑↓←→↑←↓↑→↓→↑←→←↓→↓←↑↓↑↓↑↓←↓

8x8 min

142

1 1 2 3 2 1 3 4

3 1 1 1 1 4 1 1

5 3 2 2 1 1 1 3

3 1 1 0 3 1 2 3

1 2 1 3 2 2 3 7

2 6 1 3 1 1 4 1

1 5 2 1 1 2 2 1

1 7 4 1 2 7 1 2

↑↓↑←↑→←↓←↑→↑←↓←↑↓↑→↑↓←→↑←→↓→←↑↓→↑←↑↓↑→↓→←↑←↓↑→←↓→←↑↓→↑←↓→↑←↓←↓↑

8x8 max

257

0 1 5 7 2 4 7 7

7 5 2 5 6 6 5 6

5 5 1 3 2 4 3 7

3 5 3 1 1 4 1 7

1 6 3 2 1 1 4 7

7 1 3 4 2 3 5 2

7 4 2 6 4 5 6 4

6 3 1 1 7 7 5 7

→↓↑←↓↑→↓←↑→↓←↑→←↓→↑↓↑←↑→↓↑↓←↑→↑←→↓←↑→↓↑←↓→↑←→←↑→↓←↓→↑↓↑↓↑↓↑→↓↑→

8x8 max

258

7 6 5 7 2 4 6 7

6 4 2 5 6 6 6 5

5 2 5 3 1 2 4 6

2 5 2 1 3 4 1 7

7 1 3 1 1 2 6 1

7 4 4 4 1 1 5 4

4 5 3 6 4 3 2 7

6 0 1 1 7 7 7 6

>^<>v^^v<^>v<>v<^>v^<^>v^<>v<>v^v^v^>v>v<^

5to. Encuentro para celebrar el ingenio de Martin Gardner

El ABC de la creación (3): imposibilidades

Pares y nones
Las reglas del juego y los primeros desafíos pueden verse en este enlace, otros desafíos pueden verse en este otro enlace.

De los dos últimos desafíos planteados en la entrada original, uno de ellos pedía pasar de la cinta vacía a una que contuviera solamente la letra A, y el otro desafío, pasar de la letra A a la letra B. En los comentarios a esa misma entrada Marcos Donnantuoni conjeturó que estos objetivos son imposibles de alcanzar; mi intención aquí es demostrar que, en efecto, son imposibles.

La demostración de ambas imposibilidades pasa por un argumento de paridad. Recordemos que la primera regla dice que donde haya dos casillas vacías es posible "crear" dos letras iguales; la segunda regla enuncia la operación inversa, dos letras iguales y consecutivas pueden ser borradas. La tercera regla dice que dos letras diferentes consecutivas (AB, por ejemplo) pueden ser cambiadas por la letra restante (en el ejemplo, una C).

Pensemos ahora en las cantidades de letras que haya en la configuración inicial, y específicamente fijémonos en sus paridades. Las dos primeras reglas no alteran la paridad de esas cantidades, ya le suman o le restan un 2 a una de ellas. La tercera regla, en cambio, cambia las tres paridades a la vez, ya que le suma un 1 a una cantidad y le resta 1 a las otras dos. Es decir, al aplicar cualquiera de las reglas, o bien las tres paridades no cambian, o bien cambian todas a la vez.

Esto significa que, si al comenzar, las cantidades de dos de las letras tenían la misma paridad (ambas cantidades eran pares o ambas eran impares) entonces a lo largo de todo el proceso esas cantidades seguirán teniendo la misma paridad (porque, en caso de cambiar, ambas paridades cambiarán al mismo tiempo); y si esas dos cantidades, al comenzar, tenían diferente paridad entonces la paridad seguirá siendo siempre diferente (por la misma razón). Podemos decir, en resumen, que las paridades relativas de las cantidades de letras no cambiarán nunca.

Ahora bien, si quisiéramos pasar de la cinta vacía a la letra A entonces al comenzar las cantidades de A y de B tendrían la misma paridad (ambas cantidades serían pares, ya que valen cero), mientras que al terminar habría una cantidad impar de A (una letra) y una cantidad par de B (cero). La paridad relativa de A y B habría cambiado, lo cual es imposible. Luego, no puede pasarse de la cinta vacía a una sola A. Lo mismo sucede si queremos pasar de A a B, porque al comenzar A y C tendrían diferente paridad (uno y cero son las cantidades iniciales de esas letras), pero al terminar tendrían la misma (cero y cero, ambas pares).

Una pregunta que queda pendiente es si vale la afirmación recíproca; es decir, si tenemos dos configuraciones de letras en las cuales las paridades relativas de A, B y C son las mismas (es decir, dos paridades que sean iguales/diferentes en una configuración son también iguales/diferentes en la otra configuración) entonces ¿es siempre posible pasar de una configuración a la otra? Creo que la respuesta es que sí, aunque no he podido encontrar una demostración elegante de ese hecho.

El ABC de la creación (2): soluciones y nuevos desafíos.

Espacio versus tiempo

Las reglas del juego y los primeros desafíos pueden verse en este enlace

Marcos Donnantuoni propone una variante para todos los desfíos que consiste en buscar la solución que ocupe el menos espacio posible, en lugar del menor tiempo. Es decir, ahora buscamos la solución que pueda ser desarrollada en la cinta de menor longitud (a igualdad en espacio, será mejor la solución en menor tiempo).

Éstas son, hasta ahora, las mejores soluciones para los tres primeros desafíos en esta variante.

(a) Pasar de la cinta vacía a ABC y (b) pasar de ABC a BCA: Las soluciones óptimas en tiempo (ambas de Marcos, con 5 pasos) son también hasta ahora las mejores en espacio, con 4 espacios cada una (no parece que se pueda mejorar). Las copio aquí:
0 ----
1 --AA
2 AAAA
3 A--A
4 ABBA
5 ABC-

0 ABC-
1 AA--
2 AAAA
3 A--A
4 ABBA
5 -CBA

(c) A partir de ABC recorrer las otras cinco permutaciones de esas letras: MFR tiene una solución en 25 pasos (óptima en tiempo) que sólo usa 5 espacios (la de Marcos, también de 25 pasos, pblicada en el entrada anterior, si no conté mal -y pude haber contado mal- usa 10 espacios):
00 ABC--
01 C-C--
02 C-CAA
03 C--BA
04 CCCBA
05 --CBA
06 --C-C
07 BBC-C
08 BA--C
09 BACCC
10 BAC--
11 B-B--
12 B-BAA
13 B--CA
14 BBBCA
15 --BCA
16 --B-B
17 AAB-B
18 AC--B
19 ACBBB
20 ACB--
21 -BB--
22 -BBBB
23 -B--B
24 -BAAB
25 --CAB

Dos nuevos desafíos:

El caminante (propuesto por Leonardo): pide hacer "caminar" una letra A n pasos hacia la derecha o hacia la izquierda. MFR pudo hacer "caminar" una A una cantidad par n de casillas, a la izquierda o a la derecha, en exactamente n pasos; por ejemplo para n = 4:

00 A----
01 AAA--
02 --A--
03 --AAA
04 ----A

"Para moverla sólo un lugar", dice MFR, "cuesta un poquito más de trabajo, a mí me salió en 5 pasos (y utilizando dos 'espacios' adicionales en sentido opuesto al que queremos 'avanzar')":
00 --A-
01 BBA-
02 BC--
03 BCAA
04 BB-A
05 ---A

Leonardo, por su parte, tiene una solución para mover A un paso a la derecha en 3 tiempos (y 4 espacios):
00 -A--
01 -ABB
02 --CB
03 --A-

Actualización del 15.11.13: Escribe Leonardo en los comentarios.
Conclusiones sobre traslados de A:
Para cualquier número n de pasos, con n par, la cantidad mínima es n.
Para cualquier número n de pasos, con n impar, la cantidad mínima es n+2.
Por otra lado, y como consecuencia de esto, dado un número n cualquiera, si se lo escribe de la forma q+w, siendo q y w enteros positivos, entonces la cantidad de pasos necesarios para moverlo n lugares será igual a la de q sumada a la de w.
En otras palabras, si definimos una función P(n) que es la mínima cantidad de pasos necesarios para trasladar una A n lugares, entonces P(n)=P(q+w)=P(q)+P(w) siempre que q+w=n.

Desafío escatológico (propuesto por Marcos): pide pasar de BABA a CACA...
...(1) en la menor cantidad de tiempo
...(2) usando el menor espacio.

Claudio Meller tiene una solución en 7 pasos y 6 espacios, y otra en 8 pasos y 5 espacios.
7 PASOS SEIS ESPACIOS
0. --BABA
1. CCBABA
2. CA-ABA
3. CA--CA
4. CACCCA
5. CAC--A
6. CACAAA
7. CACA

8 PASOS CINCO ESPACIOS
0. -BABA
1. --CBA
2. CCCBA
3. C--BA
4. CAABA
5. CA-CA
6. CA--B
7. CACCB
8. CACA-

La solución ¿óptima? de Marcos tiene 6 pasos y 5 espacios:
0 BABA-
1 BAC--
2 BACAA
3 B - BAA
4 B--CA
5 BAACA
6 -CACA

El ABC de la creación

Tres simples reglas para un pequeño Big Bang
(Ésta es la transcripción de mi charla en el 4º Encuentro para Celebrar el Ingenio de Martin Gardner y Jaime Poniachik.)

El universo en el que transcurre este pequeño Big Bang es una cinta dividida en casillas todas iguales; es necesario aclarar que la cinta es infinita, en el sentido de que puede ser prolongada indefinidamente por cualquiera de sus dos extremos:

Este universo contiene solamente tres tipos de partículas, a las que llamaremos A, B y C. Una "ley natural" dice que cada casilla puede contener como máximo una partícula.

Hay tres reglas que rigen el modo en el que las partículas son creadas o destruidas. Estas reglas están resumidas en la siguiente imagen:

Regla 1: En dos casillas vacías consecutivas pueden colocarse dos letras iguales (en la imagen se ejemplifica con AA, pero también puede ser BB o CC).

Regla 2: Es la inversa de la anterior; dos letras iguales consecutivas pueden ser borradas (como antes, en la imagen se ejemplifica con AA, pero también puede ser BB o CC):

Reglas 3: Dos letras diferentes consecutivas pueden ser reemplazadas por la tercera letra, es decir, las dos letras se borran y el lugar que ocupaba una de ellas pasa a ser ocupado por la otra letra. En la imagen se ejemplifica el reemplazo de AB por C, pero también vale para reemplazar BA por C, CA por B, AC por B, etc.

Veamos un ejemplo de aplicación de las reglas:

En el ejemplo hemos partido del universo vacío y hemos llegado a la configuración A-espacio-B-espacio-C. Esto se ha conseguido en seis pasos; un "paso" consiste siempre en la aplicación de una de las tres reglas.

En los desafíos se parte de una cierta configuración y se debe llegar a otra, siempre en la menor cantidad posible de pasos. Los desafíos están resumidos en esta imagen:

Desafío (a): Partir del espacio vacío y llegar a ABC (sin espacios intermedios). Se entiende que al terminar la cinta sólo muestra ABC, el resto del universo está vacío. Yo lo logré en 10 pasos, pero la solución no es necesariamente la óptima. De hecho, la noche misma del encuentro Pablo Coll me aseguró que había encontrado una solución en solamente 6 pasos y que después me la enviaría.

Desafío (b): Partir de ABC y llegar a BCA; las tres letras finales no tienen por qué ocupar las mismas casillas que las iniciales. Yo lo logré en 10 pasos, pero la solución no es necesariamente la óptima.

Desafío (c): Partir de ABC y lograr que se vayan formando sucesivamente las otras cinco permutaciones posibles de esas tres letras (ACB, BCA, BAC, CAB y CBA, no necesariamente en ese orden). En su momento, cada permutación debe aparecer sola en la cinta; la cuenta de los pasos termina en el momento en que aparece la sexta permutación (sea cual fuere). ~~Yo lo logré en 23 pasos, la solución tampoco es necesariamente la mejor.~~

En los dos últimos desafíos, para hacerlos más interesantes, no doy cantidades de pasos:

Desafío (d): Partir de la cinta vacía y llegar a A.

Desafío (e): Partir de A y llegar a B (la B no debe ocupar necesariamente la misma casilla que la A).

Las soluciones que lleguen (por mail o dejadas en los comentarios) serán publicadas aquí mismo, más abajo.

Gracias... ¡y que se diviertan!

Soluciones:
(a) Pablo Rowies dio en los comentarios una solución para el desafío (a) en 8 pasos que Claudio Meller, también en los comentarios, mejora a 6 pasos y Marcos Donnantuoni, a 5:
0 - - - -
1 - - AA
2 AAAA
3 A - - A
4 ABBA
5 ABC

(b) Pablo Rowies da una solución en 8 pasos para el desafío 2 que Claudio Meller mejora a 6 pasos y Marcos Donnantuoni, a 5:
0 ABC -
1 AA - -
2 AAAA
3 A - - A
4 ABBA
5 - CBA

(c) Marcos Donnantuoni y Claudio Meller encuentran soluciones con 25 pasos, tras un estudio informático Marcos aclara que la solución es óptima.
0__________ABC__
1__________ABCBB
2__________ABA_B
3__________AC__B
4__________ACBBB
5__________ACB__ *
6___________BB__
7_________BBBB__
8_________B__B__
9_________BAAB__
10________BAC___ *
11________BB____
12________BBBB__
13________B__B__
14________BCCB__
15________BCA___ *
16______CCBCA___
17______CCB_B___
18______CA__B___
19______CABBB___
20______CAB_____ *
21______CC______
22____CCCC______
23____C__C______
24____CBBC______
25____CBA_______ *

Sólo quedan abiertos los desafíos (d) y (e).

Soluciones óptimas:
Desafío (a): 5 pasos (Marcos Donnantuoni), no puede mejorarse.
Desafío (b): 5 pasos (Marcos Donnantuoni), no puede mejorarse.
Desafío (c): 25 pasos (Claudio Meller y Marcos Donnantuoni), no puede mejorarse.

Gracias por los comentarios en los que se plantean otros desafíos, en breve los incorporaré a una nueva entrada sobre el tema. Por supuesto, también agradezco los comentarios con soluciones, las que corresponde a los nuevos desafíos también aparecerán próximamente en otra entrada sobre este tema.

Éste es el video de la charla.

Caminata marciana (5): dos nuevos desafíos

(Viene de Caminata marciana.)

La diagonal

Éste desafío, propuesto por Rodolfo Kurchan, pide dibujar una caminata marciana que deje a los números del 0 al 8 orientados en diagonal (como se ve en el dibujo) de modo tal que la suma de los números restantes sea la mínima posible.

Rodolfo tiene una solución con una suma de 36 que se puede ver en los comentarios y que probablemente pueda mejorarse. Actualización: Marcos Donnantuoni lo mejora a 33 (la solución está en los comentarios).

N veces N

Éste desafío, propuesto por Marcos Donnantuoni pide hallar una caminata marciana en la que el 4 aparezca exactamente cuatro veces (siempre de modo tal que la suma de los números restantes sea la mínima posible), otra en la que el 5 aparezca exactamente cinco veces, otra para el 6 y otra para el 7.

El desafío para el 8 es imposible (no puede haber más que un número 8) y para el 1, 2 y 3, dice Marcos, es demasiado trivial.

Las mejores soluciones que encontró Marcos tienen sumas de 4, 8, 12 y 22 para los desafíos correspondientes a 4, 5, 6 y 7 respectivamente. Todas pueden verse en los comentarios. ¿Podrán mejorarse?

Caminata marciana (4): nuevo desafío

(Viene de Caminata marciana.)

Marcos Donnantuoni me envía por línea privada un desafío que a su vez le comunicó Pablo Coll: hallar una caminata marciana que deje exactamente un 8, dos 7, tres 6, y así sucesivamente hasta ocho 1 (además del inevitable 0 inicial).

El desafío, como digo, es hallar una caminata así, o bien demostrar que no existe ninguna. Marcos reconoce que por ahora no ha podido resolverlo.

Caminata marciana (3): Tres conjeturas y el Triángulo de Kurchan

(Viene de Caminata Marciana. Al día siguiente de la publicación inicial de la entrada hice un agregado al texto, este agregado aparece en azul.)

1. Tres conjeturas

Rodolfo Kurchan me ha hecho llegar por línea privada la siguiente conjetura:

Conjetura de Kurchan: Fijado un par de números n y m, en todas las caminatas marcianas que recorran completamente el rectángulo de n x m la suma de los números obtenidos será la misma. (No se obtendrán necesariamente los mismos números, pero sí será la misma la suma de todos ellos).

Por ejemplo, todas las caminatas marcianas que recorren el cuadrado de 3 x 3 suman 20.

Podemos extender la conjetura de la siguiente manera:

Conjetura ampliada: Fijada una región R del cuadriculado que pueda ser recorrida completamente por una caminata marciana, en todas las caminatas marcianas que recorran completamente R la suma de los números obtenidos será la misma.

La conjetura ampliada puede extenderse más todavía. Tomemos, por ejemplo, un grafo que admita un camino hamiltoniano (es decir, un camino que visite todos los nodos del grafo exactamente una vez cada uno, entendiendo que no vuelve al nodo inicial). A cada nodo del grafo le asignamos un número siguiendo el orden en que fue visitado y según la regla de la caminata marciana: cuando el camino pasa por un nodo, éste recibe el número que indica la cantidad de números que están conectados con él en ese momento. Un ejemplo:

Conjetura para grafos: Si G es un grafo que admite un camino hamiltoniano, entonces en todos los caminos hamiltonianos de G la suma de los números obtenidos será la misma.

Hay una demostración bastante simple (una vez que a uno se le ocurre) de la conjetura para grafos. Esta conjetura, como es evidente, tiene a las otras dos como casos particulares. Dejo, para quienes les interesen esas cosas, el desafío de encontrar la demostración. Una pista: la suma que se obtiene es la cantidad de lados del grafo. De este modo las tres conjeturas pasan a ser "teoremas", pero seguiré llamándolas "conjeturas" de todos modos.

2. El Triángulo de Kurchan

La conjetura de Kurchan nos habilita para construir el siguiente cuadro:

En la posición (n,m) del cuadro ponemos la suma de una caminata marciana que recorra completamente el rectángulo de n x m. (Por supuesto, el cuadro sigue infinitamente hacia la derecha y hacia abajo, aquí sólo hemos mostrado un fragmento.) Rodolfo prefiere girar el cuadro 45° y disponer los números en un triángulo al que (en analogía con el Triángulo de Pascal) llamaremos el Triángulo de Kurchan:

Rodolfo ha investigando el triángulo y encontró en él algunas propiedades curiosas. He aquí una lista:

1. La primera diagonal se obtiene sumando 1 cada vez, la segunda se obtiene sumando 5, la siguiente sumando 9, la siguiente sumando 13, etc.

2. En la segunda columna del triángulo aparece la sucesión 1, 11, 29, 55, 89,... que es http://oeis.org/search?q=1%2C11%2C29%2C55%2C89&sort=&language=english

3. La suma de los cuatro vecinos a cada "agujero" de la columna central (por ejemplo: 0 + 1 + 1 + 6 = 8; 6 + 11 + 11 + 20 = 48;...) forman la sucesión 8, 48, 120, 224,... que corresponde a los óctuples de los números hexagonales. Véase también: http://oeis.org/search?q=8%2C48%2C120%2C224%2C360%2C528&sort=&language=english

4. La diagonal a "salto de caballo" 0, 11, 38, 81,... es http://oeis.org/search?q=0%2C11%2C38%2C81&sort=&language=english

5. La suma de lo números en cada fila da 0, 2, 10, 28, 60, 110, 182,... que es el doble de la suma de los n primeros cuadrados consecutivos. Véase: http://oeis.org/search?q=2%2C10%2C28%2C60%2C110%2C182%2C280&sort=&language

6. Elijamos un número cualquiera del triángulo, pero que no esté en el borde. Tomemos sus dos vecinos de la izquierda y de la derecha, el número que está justo arriba del elegido y el que está justo abajo. La suma de esos cuatro números será el cuádruple del número elegido. Por ejemplo, si elegimos el 11 tenemos que 3 + 11 + 1 + 29 = 44 = 4 x 11.

7. Si sumamos cada número de la columna central con su vecino de abajo a la izquierda obtenemos: 0 + 1 = 1; 6 + 11 = 17; 20 + 29 = 49;... que es la sucesión de los números hexadecagonales centrados. Véase: http://oeis.org/search?q=1%2C17%2C49%2C97&sort=&language=english

Por supuesto, están todos invitados a encontrar otras propiedades u otros datos curiosos del Triángulo de Kurchan.

Caminata marciana (2)

(Viene de la entrada Caminata Marciana.)

Claudio Meller (autor, entre otras cosas, de este excelente blog) propone este desafío: hallar una caminata marciana que dibuje la siguiente espiral de 0 a 8, de modo que los números adicionales sumen lo menos posible.

Claudio tiene una solución que da una suma de 25, que puede verse en este enlace.

También propone hallar una caminata marciana que dibuje una de 8 a 0, siempre de modo que los números adicionales sumen lo menos posible.

Para este segundo desafío Claudio tiene una solución que suma 24, y que puede verse en este enlace.

Resumen de las mejores marcas hasta ahora:

Para el primer desafío: suma 18 (Marcos Donnantuoni).
Para el segundo desafío: suma 16 (Rodolfo Kurchan y Marcos Donnantuoni).

Todas las soluciones pueden verse en los comentarios a la entrada.

Caminata marciana

Ésta es el video de mi charla en el Tercer Encuentro por Martin Gardner y Jaime Poniachik:

Y ésta es la transcripción aproximada:

En esta ocasión voy a invitarlos a pasear por Marte... ¿Qué es Marte? "Un planeta" me responderán ustedes, con toda razón. Pero para nosotros el mapa de ese planeta será un cuadriculado ilimitado que sigue infintamente en todas direcciones.

Un camino en ese cuadriculado será cualquier recorrido que comience en una casilla y termine en otra (todos nuestros caminos tendrán un comienzo y un final, ninguno seguirá indefinidamente), que pase de cada casilla a otra que sea vecina en horizontal, vertical o diagonal, y que nunca pase dos veces por la misma casilla.

En la siguiente figura vemos un ejemplo de camino (el circulito rojo indica su comienzo y la flecha indica el final).

Una vez que hemos dibujado el camino, en las casillas visitadas por él (y sólo en esas) vamos a colocar números. Los números serán colocados en el mismo orden en que las casillas fueron visitadas por el camino y de acuerdo con la siguiente regla: en cada casilla va el número que indica la cantidad de números que, hasta ese momento, hay alrededor de la casilla.

En el ejemplo anterior, la primera casilla (la del circulito) no tiene todavía número alrededor, de modo que allí va un 0 (la primera casilla siempre tendrá un 0).

La siguiente casilla tiene ahora un número a su alrededor (el 0 que acabamos de poner), de modo que en la segunda casilla va un 1. La siguiente tendrá un 2, y así sucesivamente. El camino, con todos los números colocados se ve así:

Éste es el mecanismo básico: dibujamos un camino y colocamos los números según la regla que acabamos de enunciar. A partir de este mecanismo podemos plantear una serie de desafíos.

Desafío 1: Dibujar un camino en el que aparezcan, al menos una vez, todos los números del 0 al 8 (es claro que el mayor número que puede aparecer es el 8).

Un ejemplo es el siguiente:

Que, al colocar los números, se ve así (he marcado en amarillo los números del 0 al 8 para que se destaquen).

Como se ve, hay muchos números adicionales (todos los que quedaron en blanco). El verdadero desafío es logar que la suma de esos números adicionales sea la mínima posible.

Desafío 1 (completo): Dibujar un camino en el que aparezcan, al menos una vez, todos los números del 0 al 8 de modo tal que la suma de los números adicionales sea la mínima posible. En el ejemplo anterior la suma es 36, esa solución puede mejorarse.

Desafío 2: Dibujar un camino en el que se forme la siguiente distribución de números, de modo tal que la suma de los números adicionales sea la mínima posible.

El interés de esta disposición de números consiste en que se trata de un cuadrado mágico: las tres filas, las tres columna y las dos diagonales suman 12.

Desafío 3 (cráteres): Un cráter es el borde de un cuadrado de n x n con sus casillas (sólo las casillas del borde) ocupadas por números todos iguales entre sí. Por ejemplo, el siguiente es un cráter de 4 x 4 con 3's:

Como antes, el objetivo es encontrar un camino que forme diferentes cráteres de modo tal que la suma de los números adicionales sea la mínima posible. Algunas marcas que he obtenido son las siguientes:

Cráter de 3 x 3 con 2's: es imposible, es decir, no existe un camino que pueda formar un cráter así. A quienes les interese los desafíos de este tipo, pueden intentar demostrar esta imposibilidad.

Cráter de 3 x 3 con 3's: Rodolfo Kurchan, organizador del encuentro, encontró una solución de suma 8:

0

1333

13 31

2333

23

Claudio Meller, en este enlace, también aporta el dibujo de una solución de suma 8.

Cráter de 3 x 3 con 4's: en un mensaje privado Rodolfo Kurchan me ha informado que encontró una solución de suma 8, pero no envía el dibujo.

Cráter de 3 x 3 con 5's: en su mensaje privado Rodolfo Kurchan me ha informado que encontró una solución de suma 15, pero tampoco tengo el dibujo de ese camino.

Cráter de 3 x 3 con 6's: es imposible, como dije antes, quienes estén interesados por desafíos de este tipo pueden intentar demostrar esta imposibilidad.

Cráteres de otros tamaños: evéanse más abajo algunas soluciones.

Existen otras disposiciones interesantes de números que también pueden plantearse como desafíos, pero lo haré más adelante, en otras entradas.

Quienes encuentren soluciones que quieran transmitir, o nuevos desafíos para plantear a partir de este mecanismo, pueden hacerlo en los comentarios a esta misma entrada. Una manera de de escribir una solución sin recurrir a un dibujo sería indicar las direcciones en que el camino se va desplazando (N = norte o arriba, NO = noroeste, O = oeste o izquierda, etc.) Desde luego, no es relevante la posición de la casilla inicial. Por ejemplo, el camino del primer ejemplo se escribiría así: SE, O, NE, SE, N, N.

Muchas gracias.

Nota: Después de haber preparado esta charla, googleando en busca de ideas similares que alguien hubiera podido tener previamente, descubrí en este enlace un mecanismo más o menos similar, aunque no igual, al que he contado aquí. Como se puede ver en el enlace, también se parte de un camino en el que se escriben números, pero en este otro caso, se pone (un poco arbitrariamente) primero un número 1 y luego se van sumando los números que quedan alrededor. Los desafíos, además, son diferentes. No obstante las diferencias, me pareció correcto mencionar la similitud de ideas.

Actualizaciones:

Cuadrado mágico (24.10.12): Claudio Meller envía una solución que da una suma de 28 para el desafío de dibujar el cuadrado mágico. Su solución puede verse en el archivo que se descarga desde este enlace. Rodolfo Kurchan tiene una solución que da una suma de 26, que es la siguiente:
121

15072

16424

31831

2341

Y que mejora a 23:
121

15072

16424

31831

241

(En los comentarios puede verse todavía otra mejora.)

Nuevo desafío (24.10.12): Rodolfo propone hallar un camino que dibuje los números 012345678 en ese orden (siempre de tal modo que la suma de los números adicionales sea la mínima posible). Rodolfo envía esta solución, que suma 20:
2221111

0123456782

12 1121

Pero Claudio Meller, en este enlace, aporta una solución con una suma de 19.

Cráteres (24.10.12): Claudio Meller envía una solución del 4x4 con 2's que da una suma de 4, el dibujo en este enlace y envía el dibujo de una solución de suma 12 para el de 4x4 de 3's, en este enlace.

Soluciones de Rodolfo Kurchan para cráteres:
...........................
4x4 dos = 5 (mejorada por la solución de Claudio Meller)

0 1

12222

2 2

2 21

2222

...........................

4x4 tres = 12 (iguala la de Claudio Meller)

0 2

133332

13 31

3123

13333

...........................

4x4 cuatros = 20

021 1

144441

4134

42541

44441

...........................
4x4 cincos = 32

1 1

1 1 031

1 55551

154151

15 3541

155551

1111
...........................

Resumen de las mejores marcas hasta ahora:

Números del 0 al 8 al menos una vez cada uno: suma 8 (de Marcos Donnantuoni, puede verse la solución en los comentarios a la entrada, Marcos conjetura que es óptima).

Cuadrado mágico: suma 22 (de Marcos Donnantuoni, puede verse la solución en los comentarios).

Números del 0 al 8 en línea (desafío propuesto por Rodolfo): suma 16 (solución de Marcos Donnantuoni, puede verse en los comentarios).

Cráter de 3x3 con 3's: suma 8 (Rodlfo Kurchan y Claudio Meller, pueden verse en la entrada).
Cráter de 3x3 con 4's: suma 8 (Rodlfo Kurchan, confiamos en su palabra).
Cráter de 3x3 con 5's: suma 15 (Rodlfo Kurchan, confiamos en su palabra y Claudio Meller que sí envía un dibujo, que puede verse en los comentarios).

Cráter de 4x4 con 2's: suma 4 (Claudio Meller, puede verse en la entrada).
Cráter de 4x4 con 3's: suma 12 (Rodlfo Kurchan y Claudio Meller, pueden verse en la entrada).
Cráter de 4x4 con 4's: suma 20 (Rodlfo Kurchan, puede verse en la entrada).
Cráter de 4x4 con 5's: suma 32 (Rodlfo Kurchan, puede verse en la entrada).