Incluímos esta nota en El Cafecito de Paulinas para todos esos padres y madres solteros o que están criando solos. Quizás todos los demás nos imaginamos que eso "hoy es tan normal" que no nos pone a pensar en todos los escollos que representan para estos padres y madres una cosa tan sencilla como un catarro o bien más simple aún el cansancio diario. En casa cuando ellos están solos con sus hijos no hay quien tome su lugar para atender a los chicos o dividirse las tareas del hogar en lo que el otro se encarga de los chicos de sus tareas y de otras mil cosas más.
En Puerto Rico la corporación Camina con Jesús publica una revista dedicada a este sector. En ella encontrarás temas relacionados con espiritualidad, valores y otros como temas legales que pueden ser de orientación inicial a los procesos legales de custodia, salud y hasta finanzas.
¿Interesado en encontrar esta revista? Contácta con sus editores en http://www.caminaconjesus.com/
O búscala pronto en Paulinas
Calle Arzuaga 164 y San Francisco Plaza Ave. De Diego... Río Piedras
787.765.4390
Un problema de probabilidades
(Esta entrada es la participación de El Topo Lógico en el Carnaval de Matemáticas.)
Imaginemos el siguiente juego de azar: se le presentan a un jugador n cajas cerradas, cada una de las cuales contiene una bola marcada con un número entre 1 a n (cajas diferentes contienen números diferentes). Las cajas son perfectamente iguales y es imposible determinar por su aspecto el contenido de cada una.
El jugador anota en la tapa de cada caja un número de 1 a n. No es obligatorio que anote números diferentes. Puede, por ejemplo, anotar un 1 en todas las cajas.
Una vez hechas las anotaciones, se destapan las cajas. El jugador se anota entonces un punto por cada caja en la que el número anotado en la tapa coincida con el número de la bola contenida.
Por ejemplo, si el jugador anota un 1 en todas las cajas entonces ganará exactamente un punto.
Preguntas:
1) Si n es par y el jugador anota un 1 en la mitad de las cajas y un 2 en la otra mitad ¿cuál es su ganancia esperada?
2) ¿Cuál es la estrategia óptima para el jugador? Es decir ¿cuál es la estrategia para la cual la ganancia esperada del jugador es la máxima posible?
Imaginemos el siguiente juego de azar: se le presentan a un jugador n cajas cerradas, cada una de las cuales contiene una bola marcada con un número entre 1 a n (cajas diferentes contienen números diferentes). Las cajas son perfectamente iguales y es imposible determinar por su aspecto el contenido de cada una.
El jugador anota en la tapa de cada caja un número de 1 a n. No es obligatorio que anote números diferentes. Puede, por ejemplo, anotar un 1 en todas las cajas.
Una vez hechas las anotaciones, se destapan las cajas. El jugador se anota entonces un punto por cada caja en la que el número anotado en la tapa coincida con el número de la bola contenida.
Por ejemplo, si el jugador anota un 1 en todas las cajas entonces ganará exactamente un punto.
Preguntas:
1) Si n es par y el jugador anota un 1 en la mitad de las cajas y un 2 en la otra mitad ¿cuál es su ganancia esperada?
2) ¿Cuál es la estrategia óptima para el jugador? Es decir ¿cuál es la estrategia para la cual la ganancia esperada del jugador es la máxima posible?
Paradojas del infinito (II)
Tenemos, por un lado, una recta infinita. Por otro lado tenemos una cantidad infinita de pequeños segmentos. Uno de estos segmentos mide 1/2 cm, otro mide 1/4 cm, otro 1/8 cm. y así sucesivamente. Aunque la cantidad de segmentos es infinita, la suma total de sus longitudes es apenas 1 cm.
Si distribuyéramos los segmentos a lo largo de la recta, la longitud total que cubrirían sería de apenas 1 cm. (o menos todavía, si los segmentos se superponen). La intuición nos dice que, no importa cómo coloquemos los segmentos, inevitablemente quedarán grandes porciones de la recta sin cubrir. Después de todo, estaríamos cubriendo apenas 1 cm. de una recta de longitud infinita.
Imaginemos que hemos colocado, de alguna forma, los infinitos segmentos sobre la recta. Tomemos ahora otro segmento de, digamos, 1 mm. de longitud. Éste será nuestro segmento de prueba.
Si al colocar el segmento de prueba sobre la recta, éste toca a alguno de los infinitos segmentos que colocamos primero, entonces sonará una alarma. Por "tocar" entendemos que haya una parte en común (que no se reduzca a un solo punto) entre alguno de los segmentos iniciales y el segmento de prueba.
La intuición nos dice que, no importa cómo hayamos colocado los segmentos iniciales (que abarcan solamente 1 cm. en una recta de longitud infinita), habrá muchas formas de colocar el segmento de prueba sin que suene la alarma.
Sin embargo... existe una manera de ubicar los segmentos iniciales de tal modo que, no importa cómo se coloque el segmento de prueba, la alarma siempre suene. Es decir, con segmentos que suman en total apenas 1 cm. de longitud es posible cubrir casi totalmente una recta de longitud infinita. Más exactamente, es posible cubrirla de tal modo que no haya en ella ni siquiera una parte de 1 mm. de longitud que quede sin ser tocada por al menos un segmento. Más aún, lo mismo sucedería si en lugar de un segmento de prueba de 1 mm. de longitud hubiéramos elegido uno de 0,000000001 mm., o cualquier otra longitud aún menor (siempre que no fuera cero).
El modo de lograr este prodigo es el siguiente. Es sabido que el conjunto de los números racionales es numerable, es decir, es posible establecer una correspondencia uno-a-uno entre el conjunto de los números racionales y el conjunto formado por 0, 1, 2, 3, 4,... Fijemos una tal correspondencia y llamemos q0 al número racional que se corresponde con el 0, q1 al que se corresponde con el 1, y así sucesivamente. (Es interesante observar que esta correspondencia puede definirse explícitamente, por lo que podríamos decir concretamente quién es q0, quién es q1, etc.)
Transformemos a la recta que teníamos al principio en una recta "numérica". Para ello marquemos dos puntos a 1 cm. de distancia entre sí, a uno de ellos asignémosle el número 0 y al otro, el número 1. De la manera usual quedan asignados todos los números racionales.
Pasemos ahora a ubicar los segmentos:
El segmento de longitud 1/2 cm. debe ser colocado cubriendo el intervalo [q0 - 1/4, q0 + 1/4].
El de longitud 1/4 cm. debe ser colocado cubriendo el intervalo [q1 - 1/8, q1 + 1/8].
El de longitud 1/8 cm. debe ser colocado cubriendo el intervalo [q2 - 1/16, q2 + 1/16].
Y así sucesivamente.
No es difícil probar que esta distribución cumple las condiciones indicadas antes: la suma total de los segmentos es 1 cm., pero no hay ninguna parte de longitud 1 mm. (o menor) que quede sin ser tocada por al menos un segmento. Para demostrar esto último, imaginemos que colocamos nuestro segmento de prueba de modo que coincida con el intervalo [a, b]. Ese intervalo (no importa su longitud, siempre que no sea nula) contiene al menos un número racional qn tal que b > qn > a. Por lo tanto, el segmento de prueba se toca con el segmento centrado en qn.
Si distribuyéramos los segmentos a lo largo de la recta, la longitud total que cubrirían sería de apenas 1 cm. (o menos todavía, si los segmentos se superponen). La intuición nos dice que, no importa cómo coloquemos los segmentos, inevitablemente quedarán grandes porciones de la recta sin cubrir. Después de todo, estaríamos cubriendo apenas 1 cm. de una recta de longitud infinita.
Imaginemos que hemos colocado, de alguna forma, los infinitos segmentos sobre la recta. Tomemos ahora otro segmento de, digamos, 1 mm. de longitud. Éste será nuestro segmento de prueba.
Si al colocar el segmento de prueba sobre la recta, éste toca a alguno de los infinitos segmentos que colocamos primero, entonces sonará una alarma. Por "tocar" entendemos que haya una parte en común (que no se reduzca a un solo punto) entre alguno de los segmentos iniciales y el segmento de prueba.
La intuición nos dice que, no importa cómo hayamos colocado los segmentos iniciales (que abarcan solamente 1 cm. en una recta de longitud infinita), habrá muchas formas de colocar el segmento de prueba sin que suene la alarma.
Sin embargo... existe una manera de ubicar los segmentos iniciales de tal modo que, no importa cómo se coloque el segmento de prueba, la alarma siempre suene. Es decir, con segmentos que suman en total apenas 1 cm. de longitud es posible cubrir casi totalmente una recta de longitud infinita. Más exactamente, es posible cubrirla de tal modo que no haya en ella ni siquiera una parte de 1 mm. de longitud que quede sin ser tocada por al menos un segmento. Más aún, lo mismo sucedería si en lugar de un segmento de prueba de 1 mm. de longitud hubiéramos elegido uno de 0,000000001 mm., o cualquier otra longitud aún menor (siempre que no fuera cero).
El modo de lograr este prodigo es el siguiente. Es sabido que el conjunto de los números racionales es numerable, es decir, es posible establecer una correspondencia uno-a-uno entre el conjunto de los números racionales y el conjunto formado por 0, 1, 2, 3, 4,... Fijemos una tal correspondencia y llamemos q0 al número racional que se corresponde con el 0, q1 al que se corresponde con el 1, y así sucesivamente. (Es interesante observar que esta correspondencia puede definirse explícitamente, por lo que podríamos decir concretamente quién es q0, quién es q1, etc.)
Transformemos a la recta que teníamos al principio en una recta "numérica". Para ello marquemos dos puntos a 1 cm. de distancia entre sí, a uno de ellos asignémosle el número 0 y al otro, el número 1. De la manera usual quedan asignados todos los números racionales.
Pasemos ahora a ubicar los segmentos:
El segmento de longitud 1/2 cm. debe ser colocado cubriendo el intervalo [q0 - 1/4, q0 + 1/4].
El de longitud 1/4 cm. debe ser colocado cubriendo el intervalo [q1 - 1/8, q1 + 1/8].
El de longitud 1/8 cm. debe ser colocado cubriendo el intervalo [q2 - 1/16, q2 + 1/16].
Y así sucesivamente.
No es difícil probar que esta distribución cumple las condiciones indicadas antes: la suma total de los segmentos es 1 cm., pero no hay ninguna parte de longitud 1 mm. (o menor) que quede sin ser tocada por al menos un segmento. Para demostrar esto último, imaginemos que colocamos nuestro segmento de prueba de modo que coincida con el intervalo [a, b]. Ese intervalo (no importa su longitud, siempre que no sea nula) contiene al menos un número racional qn tal que b > qn > a. Por lo tanto, el segmento de prueba se toca con el segmento centrado en qn.
La Paradoja de Banach-Tarski (Cap. 2)
(Para ver los sucesivos capítulos de esta saga haga clic sobre la etiqueta Banach-Tarski.)
Cortar y Pegar
En este capítulo vamos a estudiar un problema de "corte y confección". La intención es comenzar a aproximarnos a una correcta interpretación del Teorema de Banach-Tarski.
Es problema dice así: ¿Es posible dividir un cuadrado en una cantidad finita de partes de tal modo que con éstas sea posible ensamblar un triángulo isósceles? (A las partes resultantes de la división se les puede aplicar rotaciones, traslaciones y simetrías, es decir, movimientos que no las deformen.)
En realidad hay dos maneras de entender este problema, las que podríamos llamar, por una lado, la interpretación concreta o física y, por el otro, la interpretación abstracta o matemática.
La interpretación concreta es la que seguramente casi todos adoptarían si intentaran resolver el problema. En esta interpretación pensamos al cuadrado como si fuera un objeto físico, un cuadrado de papel, por ejemplo, que tenemos que cortar con una tijera. Con las partes resultantes, cual si fueran piezas de un rompecabezas, debemos armar un triángulo iósceles.
Como se ve en el dibujo siguiente, el problema así interpretado se resuelve fácilmente. Sólo debemos cortar el cuadrado por una de sus diagonales.
 En la interpretación abstracta vemos al cuadrado como un conjunto de puntos del plano. Dividir el cuadrado en partes equivale, en este caso, a establecer aquello que en la Teoría de Conjuntos se llama una partición del conjunto. Es decir, dividimos el cuadrado en subconjuntos de tal modo que cada punto pertenezca a uno y sólo uno de los subconjuntos de la partición.
En la interpretación abstracta vemos al cuadrado como un conjunto de puntos del plano. Dividir el cuadrado en partes equivale, en este caso, a establecer aquello que en la Teoría de Conjuntos se llama una partición del conjunto. Es decir, dividimos el cuadrado en subconjuntos de tal modo que cada punto pertenezca a uno y sólo uno de los subconjuntos de la partición.

Cortar y Pegar
En este capítulo vamos a estudiar un problema de "corte y confección". La intención es comenzar a aproximarnos a una correcta interpretación del Teorema de Banach-Tarski.
Es problema dice así: ¿Es posible dividir un cuadrado en una cantidad finita de partes de tal modo que con éstas sea posible ensamblar un triángulo isósceles? (A las partes resultantes de la división se les puede aplicar rotaciones, traslaciones y simetrías, es decir, movimientos que no las deformen.)
En realidad hay dos maneras de entender este problema, las que podríamos llamar, por una lado, la interpretación concreta o física y, por el otro, la interpretación abstracta o matemática.
La interpretación concreta es la que seguramente casi todos adoptarían si intentaran resolver el problema. En esta interpretación pensamos al cuadrado como si fuera un objeto físico, un cuadrado de papel, por ejemplo, que tenemos que cortar con una tijera. Con las partes resultantes, cual si fueran piezas de un rompecabezas, debemos armar un triángulo iósceles.
Como se ve en el dibujo siguiente, el problema así interpretado se resuelve fácilmente. Sólo debemos cortar el cuadrado por una de sus diagonales.
Intentemos, para esta interpretación, la misma solución de antes. Dividimos el cuadrado por la diagonal, pero en este caso cada punto de esa diagonal sólo puede estar en uno de los dos triángulos resultantes. En la solución física había una duplicación: cada punto de la diagonal aparecía en ambos catetos de los triángulos resultantes de la división.
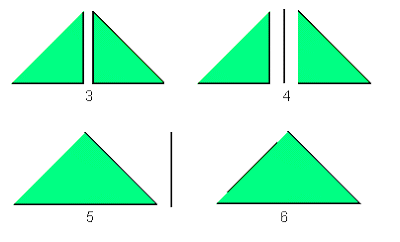
En el paso 2 del dibujo vemos que la hipoptenusa del triángulos inferior no está marcada de color negro. Esto indica que a ese triángulo "le falta" su hipotenusa (y por lo tanto, la figura en realidad no es un triángulo, ya que entendemos que un triángulo debe incluir todos sus lados).
Al ensamblar las piezas debemos tener la precaución inversa: cada punto de la figura final debe provenir de uno y sólo uno de los puntos de las piezas reunidas. Al intentar reunir los dos triángulos (véase el paso 3 en el dibujo siguiente) los catetos no pueden superponerse pues habría una duplicación.
"Cortamos" entonces el cateto de uno de los triángulos y lo separamos como una pieza más (paso 4). Reunimos entonces los dos triángulos (paso 5), pero la figura resultante todavía no es un triángulo completo, ya que le falta un lado. Podemos intentar completarlo con el segmento antes separado (paso 6), pero, Pitágoras mediante, ese lado es más corto que el segmento faltante, por lo que la figura final todavía queda incompleta (no es en realidad un triángulo).
En definitiva, según la interpretación abstracta, no hemos podido resolver el problema ya que no logramos armar un triángulo isósceles completo.
¿Es posible resolver el problema según la interpretación abstracta? Dejo la pregunta para los lectores.
Me interesa destacar aquí que el intento de solución según la interpretación abstracta nos ha mostrado una división en partes que es irrealizable en la práctica. El paso 4 (y, de hecho, también el paso 2) son imposibles en la realidad física ya que no existe en el mundo físico el equivalente exacto de un segmento matemático. Existen varillas delgadas, líneas en el papel y otros objetos que podemos imaginar como cercanos a un segmento, pero que de ninguna manera lo son, ya que en todos los casos se trata de cuerpos físicos tridimensionales formados por una cantidad finita de átomos.
Como ya se adivina, el Teorema de Banach-Tarski (que dice que una esfera se puede dividir en cinco partes que, a su vez, permiten ensamblar dos esferas iguales a la original) se refiere a una división abstracta o matemática irrealizable en la práctica.
(Continuará...)
La Paradoja de Banach-Tarski (Cap. 1)
(Para ver los sucesivos capítulos de esta saga haga clic sobre la etiqueta Banach-Tarski.)
Introducción
Hace algún tiempo (véase aquí) escribí en este mismo blog una entrada en la que comentaba que la palabra paradoja suele usarse en muchos y diversos sentidos (no equivalentes, e incluso contradictorios, entre sí). Uno de estos muchos significados podría resumirse de esta manera: hecho matemático perfectamente válido, pero totalmente contrario a nuestra intuición (por así decirlo, un hecho que la intuición nos dice que debería ser falso, pero que la razón matemática demuestra, en cambio, que es verdadero). Por ejemplo, la palabra paradoja es usada con esta acepción cuando se habla de la llamada Paradoja de Banach-Tarski.
Se le da el nombre de Paradoja de Banach-Tarski a un teorema totalmente válido, que fue correctamente demostrado en los primeros años del siglo XX por los matemáticos polacos Stephan Banach y Alfred Tarski, pero cuyo enunciado es, por decir poco, muy sorprendente.
El teorema dice así: cualquier esfera maciza puede cortarse en cinco partes que, al ser rotadas y trasladadas convenientemente (sin deformarlas), permiten ensamblar dos esferas macizas cada una de ellas iguales a la esfera inicial.
¡La duplicación de la esfera! Cortamos una esfera en cinco partes y con ellas armamos dos esferas iguales a la inicial. Sin agregar materia hemos duplicado el volumen que teníamos inicialmente.
Dejemos volar la imaginación: tomemos una pequeña esfera de oro, apliquemos el proceso de duplicación de Banach-Tarski y tendremos (sin agregar oro adicional) dos esferas de oro iguales a la inicial. Apliquemos el proceso a cada una de estas dos esferas y tendremos cuatro, y luego ocho, y luego... Al cabo de unos cuantos pasos estaremos literalmente nadando en oro. O podemos hacerlo con una esfera de pan y así terminaríamos con el hambre en el mundo.
¿Es esto posible? ¿Podemos duplicar el oro o el pan? Obviamente no, pero el teorema dice que sí podemos. ¿Cómo se explica esa discrepancia? La idea de esta saga es estudiar precisamente estas cuestiones. No sé si llegaremos a ver la demostración del teorema en sí, pero sí me interesa analizar qué es exactamente lo que en verdad dice el teorema y por qué, a pesar de que es verdadero matemáticamente, no es aplicable a esferas físicas de oro o de pan.
En última instancia, se trata también de internarnos un poco en la espinosa cuestión de la relación entre la Matemática y la Física.
(Continuará...)
Introducción
Hace algún tiempo (véase aquí) escribí en este mismo blog una entrada en la que comentaba que la palabra paradoja suele usarse en muchos y diversos sentidos (no equivalentes, e incluso contradictorios, entre sí). Uno de estos muchos significados podría resumirse de esta manera: hecho matemático perfectamente válido, pero totalmente contrario a nuestra intuición (por así decirlo, un hecho que la intuición nos dice que debería ser falso, pero que la razón matemática demuestra, en cambio, que es verdadero). Por ejemplo, la palabra paradoja es usada con esta acepción cuando se habla de la llamada Paradoja de Banach-Tarski.
Se le da el nombre de Paradoja de Banach-Tarski a un teorema totalmente válido, que fue correctamente demostrado en los primeros años del siglo XX por los matemáticos polacos Stephan Banach y Alfred Tarski, pero cuyo enunciado es, por decir poco, muy sorprendente.
El teorema dice así: cualquier esfera maciza puede cortarse en cinco partes que, al ser rotadas y trasladadas convenientemente (sin deformarlas), permiten ensamblar dos esferas macizas cada una de ellas iguales a la esfera inicial.
¡La duplicación de la esfera! Cortamos una esfera en cinco partes y con ellas armamos dos esferas iguales a la inicial. Sin agregar materia hemos duplicado el volumen que teníamos inicialmente.
Dejemos volar la imaginación: tomemos una pequeña esfera de oro, apliquemos el proceso de duplicación de Banach-Tarski y tendremos (sin agregar oro adicional) dos esferas de oro iguales a la inicial. Apliquemos el proceso a cada una de estas dos esferas y tendremos cuatro, y luego ocho, y luego... Al cabo de unos cuantos pasos estaremos literalmente nadando en oro. O podemos hacerlo con una esfera de pan y así terminaríamos con el hambre en el mundo.
¿Es esto posible? ¿Podemos duplicar el oro o el pan? Obviamente no, pero el teorema dice que sí podemos. ¿Cómo se explica esa discrepancia? La idea de esta saga es estudiar precisamente estas cuestiones. No sé si llegaremos a ver la demostración del teorema en sí, pero sí me interesa analizar qué es exactamente lo que en verdad dice el teorema y por qué, a pesar de que es verdadero matemáticamente, no es aplicable a esferas físicas de oro o de pan.
En última instancia, se trata también de internarnos un poco en la espinosa cuestión de la relación entre la Matemática y la Física.
(Continuará...)